１次元CNNで波形データを分類

Pythonで波形データを分類する方法を解説します。

データセット

load_japanese_vowels

データセットは、scikit-learnにあるload_japanese_vowelsを使います。

!pip install -Uqqq sktime
from sktime.datasets import load_japanese_vowels
import numpy as np
import pandas as pd

data = load_japanese_vowels()
df = data[0]
df["label"] = data[1].astype(np.uint8) - 1

df.head()

このようにdim0~11の特徴量と、波の種類を示すlabelが入っています。

１行目のデータを見てみましょう。

import matplotlib.pyplot as plt
plt.figure(figsize = (8, 4))
for i in range(12):
    plt.plot(df[f"dim_{i}"].values[0].values)
plt.show()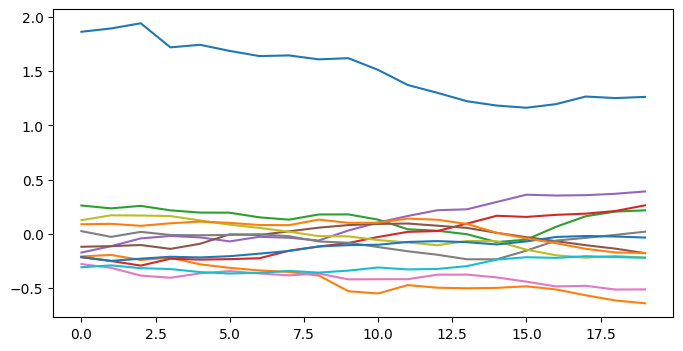

こんな感じで12列の波形データとなっています。
１行目のlabelは０なので、上図の波形からラベルが０であることを予測できれば成功ですね。

データ分割

モデルを作成する際は、データを学習用と検証用とにわけて使います。
そのために各業に分割番号を付与していきましょう。

from sklearn.model_selection import StratifiedKFold
df["fold"] = -1
skf = StratifiedKFold(n_splits = 5, shuffle = True, random_state = 0)
for fold, (_, valid_idx) in enumerate(skf.split(df, df["label"])):
    df.loc[valid_idx, "fold"] = fold
print(df["fold"].value_counts().sort_index())

# ==========output==========
# fold
# 0    128
# 1    128
# 2    128
# 3    128
# 4    128

StratifiedKFoldで５分割しました。StratifiedKFoldはラベルの分布を保ったまま分割してくれます。
詳しくは、交差検証でよく使うデータ分割法４つをご覧ください。

データセットの定義

今回はpytorchで分類モデルを作ります。
pytorchを使う場合、データを取り出すクラスを定義しなければなりません。
詳しくは、pytorchで機械学習モデルを作る方法をご覧ください。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader

class Data(Dataset):
    #初期条件
    def __init__(self, data):
        self.data = data
        self.max_len = 30
        self.columns = [f"dim_{i}" for i in range(12)]

    #データセットの長さ（行数）
    def __len__(self):
        return len(self.data)

    #データの取り出し(idxは行番号)
    def __getitem__(self, idx):
        waves = self.data[self.columns].values[idx]
        x = np.stack([w.values for w in waves], axis = 0)
        for i in range(x.shape[0]):
            _x = x[i]
            _x = (_x - _x.min()) / (_x.max() - _x.min())
            x[i] = _x
        if x.shape[1] < self.max_len:
            pad = np.zeros((x.shape[0], self.max_len - x.shape[1]))
            x = np.concatenate([x, pad], axis = 1)
        x = torch.from_numpy(x.astype(np.float32))

        y = self.data["label"].values[idx]
        y = torch.tensor(y, dtype = torch.long)

        return {"x": x, "y": y}

こんな感じでDatasetを使って定義します。
１行について12個の波形データがあるので、それらをnp.stackで重ねて出力しましょう。

試しにデータを取り出してみます。

ds = Data(df)
dl = DataLoader(ds, batch_size = 4, shuffle = True)
b = next(iter(dl))
x = b["x"]
y = b["y"]
print(x.shape)
print(y)

# ==========output==========
# torch.Size([4, 12, 30])
# tensor([4, 1, 2, 6])

xが波形データで、サイズは(バッチサイズ, 波形の数, 波形の長さ)です。
yがラベルで、今回出力されたデータは(4, 1, 2, 6)の波形でした。

こんな感じでデータを小出しするデータローダーが定義できればＯＫです。

モデルの定義

pytorchでモデルを定義しましょう。

class Net(nn.Module):
    #初期条件
    def __init__(self):
        super().__init__()
        #１次元畳み込み層
        self.cnn0 = nn.Conv1d(in_channels = 12, out_channels = 32, kernel_size = 7, stride = 1, padding = (7 - 1) // 2)
        self.cnn1 = nn.Conv1d(in_channels = 32, out_channels = 64, kernel_size = 5, stride = 1, padding = (5 - 1) // 2)
        self.cnn2 = nn.Conv1d(in_channels = 64, out_channels = 64, kernel_size = 3, stride = 1, padding = (3 - 1) // 2)
        #分類層
        self.head = nn.Linear(64, 9)

    #モデル実行
    def forward(self, x):
        #波形データの特徴量抽出
        x = F.relu(self.cnn0(x))
        x = F.relu(self.cnn1(x))
        x = F.relu(self.cnn2(x))
        #長さ方向に平均
        x = x.mean(dim = -1)
        #分類
        x = self.head(x)
        return x

out_channelsが大きいほどたくさんの特徴量を作ることができます。
また、kernel_sizeが大きいほど長い範囲での特徴を捉えます。これは長すぎても短すぎてもダメです。

最後に長さ方向の平均をとることで、out_channels(=64)の次元数にまとまります。
Linear層に通して予測ラベルにしましょう。

動かしてみると以下の通り。

model = Net()
print(model(x).detach().numpy().shape)

# ==========output==========
# (4, 9)

4がバッチサイズ、9がラベル数です。

学習と検証

学習と検証のサイクルを実行しましょう。

#検証用に割り当てする番号
fold = 0
#学習データ
train = df.loc[df.fold != fold].reset_index(drop = True)
train_ds = Data(train)
train_dl = DataLoader(train_ds, batch_size = 8, shuffle = True, drop_last = True)
#検証データ
valid = df.loc[df.fold == fold].reset_index(drop = True)
valid_ds = Data(valid)
valid_dl = DataLoader(valid_ds, batch_size = 8, shuffle = True, drop_last = False)

#モデル
model = Net()
#最適化手法
optimizer = torch.optim.Adam(model.parameters(), lr = 1e-3)
#損失関数
criterion = nn.CrossEntropyLoss()

fold=0のデータを検証用に割り当て、他は学習用にしました。
データローダーの定義までしておきましょう。

次に、最適化手法と損失関数を定義します。
最適化手法はAdamが無難です。損失関数は他クラス分類ならCrossEntropyLossを使いましょう。

では、学習を検証を実行してみます。

history = {"train": [], "valid": []}
#epochの数だけ繰り返す
for epoch in range(40):
    #学習
    train_loss = 0
    for b in train_dl:
        #波形データ
        x = b["x"]
        #ラベル
        y = b["y"]
        #予測
        logits = model(x)
        #誤差計算
        loss = criterion(logits, y)
        train_loss += loss.item() * len(x)
        #誤差伝播
        loss.backward()
        #更新
        optimizer.step()
        optimizer.zero_grad()
    history["train"].append(train_loss / len(train_ds))

    #検証
    valid_loss = 0
    for b in valid_dl:
        x = b["x"]
        y = b["y"]
        with torch.no_grad():
            logits = model(x)
            loss = criterion(logits, y)
        valid_loss += loss.item() * len(x)
    history["valid"].append(valid_loss / len(valid_ds))

plt.plot(history["train"], label = "train")
plt.plot(history["valid"], label = "valid")
plt.legend()
plt.show()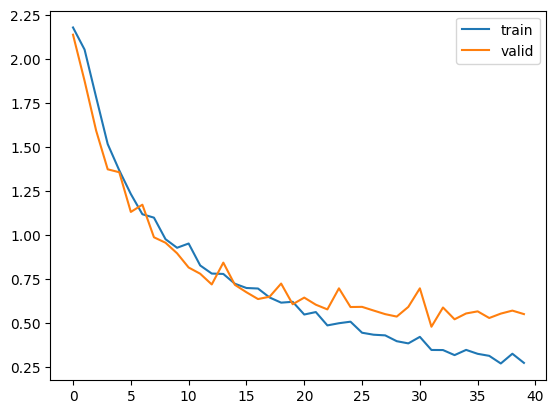

上図のように徐々に誤差が減少していたら成功です。

予測

実際に予測してみましょう。

from sklearn.metrics import accuracy_score

preds = []
trues = []
for b in valid_dl:
    x = b["x"]
    y = b["y"]
    with torch.no_grad():
        logits = model(x).softmax(dim = 1).numpy().argmax(axis = 1)
    preds += logits.tolist()
    trues += y.tolist()
print(accuracy_score(trues, preds))

# ==========output==========
# 0.7421875

検証用データで各波形の予測値を計算します。
softmaxに通すことで、9つあるラベルのどれに該当するかを確率で表すことができます。

予測したラベル(preds)と正解のラベル(trues)の正解率を計算するため、accuracy_scoreを使いましょう。
今回の正解率は約74%でした。

もっと正解率を上げるアイデアとしては、
・out_channelsやkernel_sizeを変えてみる
・Conv1dの総数を増やしてみる
・Epoch数を増やしてみる
などいろいろありますね。