
Pythonで機械学習を始めたいけど、
何から勉強すれば良いかわからない。。。
という方は、まずは線形回帰から始めてみましょう。
めちゃくちゃシンプルなので機械学習の初心者でも実装可能です。
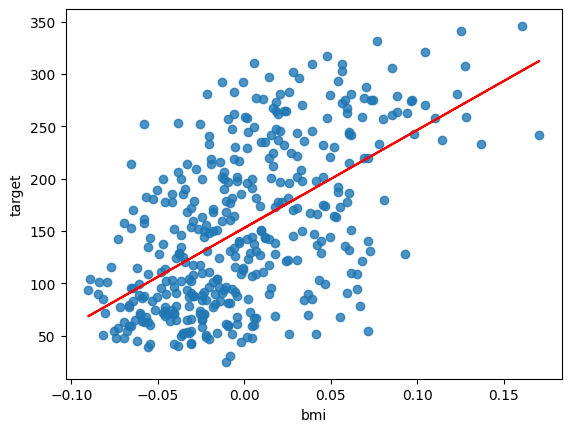
簡単に言うと、こんな感じのちょうど良い線を引いて予測するモデルです。
データセット

そもそも使えそうなデータを持っていない。。。
という人でも大丈夫です。scikit-learnにサンプルデータがあります。
Python実行環境がない方はGoogle Colaboratoryを使いましょう。
>>Google Colaboratoryの使い方
import pandas as pd
from sklearn.datasets import load_diabetes
data = load_diabetes()
df = pd.DataFrame(data["data"], columns = data["feature_names"])
df["target"] = data["target"]
df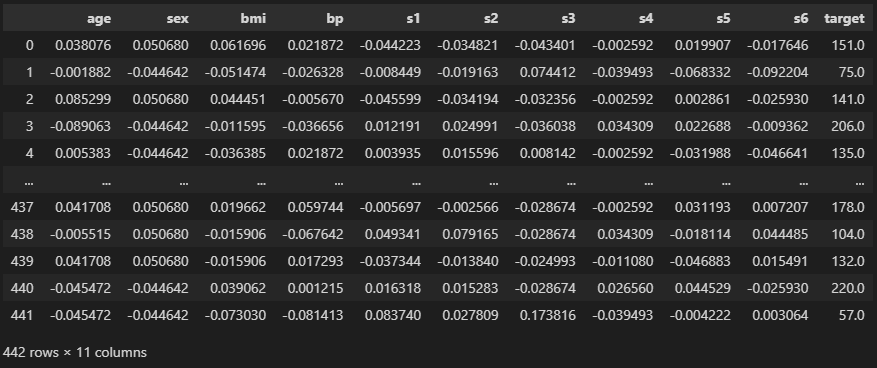
“load_diabetes”というデータセットです。
“target”が予測したい値です。
import matplotlib.pyplot as plt
plt.scatter(df["bmi"], df["target"], alpha = 0.5)
plt.xlabel("bmi")
plt.ylabel("target")
plt.show()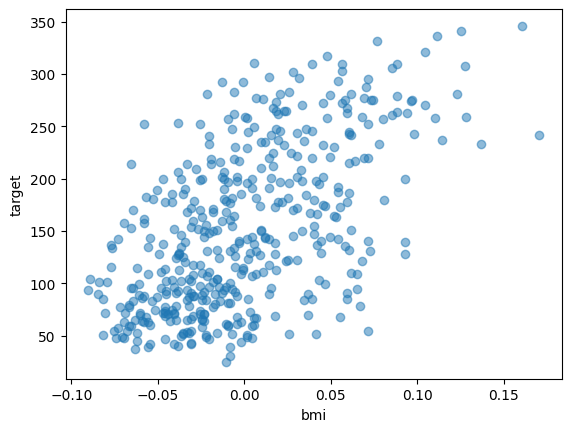
このようにtargetはbmiと相関がありそうです。
データ分割
from sklearn.model_selection import train_test_split
train, test = train_test_split(df, test_size = 0.1)
print(df.shape, train.shape, test.shape)
# ========== output ==========
# (442, 11) (397, 11) (45, 11)モデルに学習させるデータと、検証に使うデータとに分けます。
train_test_splitで分割しましょう。
test_size = 0.1にすると10%が検証データになります。
【関連記事】交差検証でよく使うデータ分割法
単回帰モデルの作成
学習
from sklearn.linear_model import LinearRegression
#学習用データ
X_train = train["bmi"].values.reshape(-1, 1)
y_train = train["target"].values
#検証用データ
X_test = test["bmi"].values.reshape(-1, 1)
y_test = test["target"].values
model = LinearRegression()
model.fit(X_train, y_train)たったこれだけです。
今回は単回帰なのでbmiのみを特徴量に使用しました。
LinearRegressionを呼び出してfitに特徴量と答えを渡すだけでOKです。
勾配と切片
print(model.coef_, model.intercept_)
# ========== output ==========
# [935.83555314] 153.18883110145993この2つの値を使って、bmiからtargetを予測してみます。
#import matplotlib.pyplot as plt
plt.scatter(X_train, y_train, alpha = 0.8)
plt.plot(X_train, X_train * 935 + 153, "r-") #coef_とintercept_から予測する式
plt.xlabel("bmi")
plt.ylabel("target")
plt.show()
bmiとtargetに対して、直線をフィットさせることができました。
なんか良さそうに引けてますが、これは学習に使ったデータ(train)だからでもあります。
精度検証
正確な精度を確かめるには、学習で教えないデータ(test)を使いましょう。
plt.scatter(X_test, y_test, alpha = 0.8)
plt.plot(X_test, X_test * 935 + 153, "r-") #coef_とintercept_から予測する式
plt.xlabel("bmi")
plt.ylabel("target")
plt.show()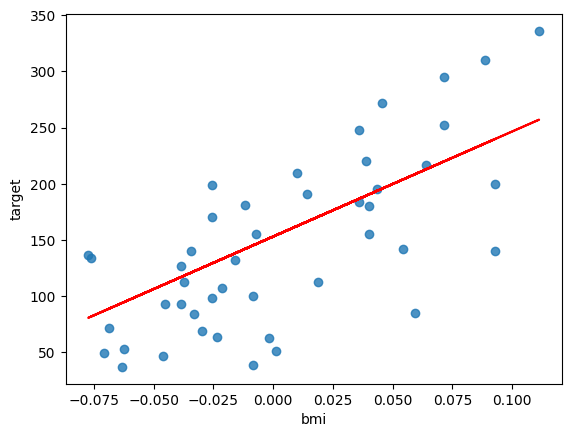
検証データでもおおよそフィットしていますね。
誤差も計算してみましょう。
import numpy as np
from sklearn.metrics import mean_squared_error
print(np.sqrt(mean_squared_error(y_test, X_test * 935 + 153)))
# ========== output ==========
# 54.93980529280439平均二乗誤差が54.9でした。
以上のように、1つの特徴で線型回帰を行う単回帰のモデルを作ることができます。
重回帰
単回帰は1つの特徴で予測しますが、できれば複数の列を考慮させたいですよね。
そんなときは重回帰を試しましょう。
データは単回帰のときと同じものを使います。
学習
まずは、使える列を抽出します。
feats = [c for c in df.columns if c != "target"]
print(feats)
# ========== output ==========
# ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']これら10個の特徴を使って学習させましょう。
#from sklearn.linear_model import LinearRegression
#学習用データ
X_train = train[feats].values
y_train = train["target"].values
#検証用データ
X_test = test[feats].values
y_test = test["target"].values
model = LinearRegression()
model.fit(X_train, y_train)単回帰と同じくfitで学習できます。
渡すデータがbmiだけだったところが、featsに変わっていますね。
精度検証
print(model.coef_)
print(model.intercept_)
# ========== output ==========
# [ -38.25073257 -256.97023749 546.91654486 345.42699846 -621.68395058
# 360.70650365 35.60090263 108.06199165 711.05104084 48.29178179]
# 152.25170953043826このように勾配(傾き)は特徴量の数10個になっています。
#import matplotlib.pyplot as plt
bmi = X_train[:, 2]
plt.scatter(bmi, y_train, alpha = 0.8)
plt.plot(bmi, bmi * model.coef_[2] + model.intercept_, "r-")
plt.xlabel("bmi")
plt.ylabel("target")
plt.show()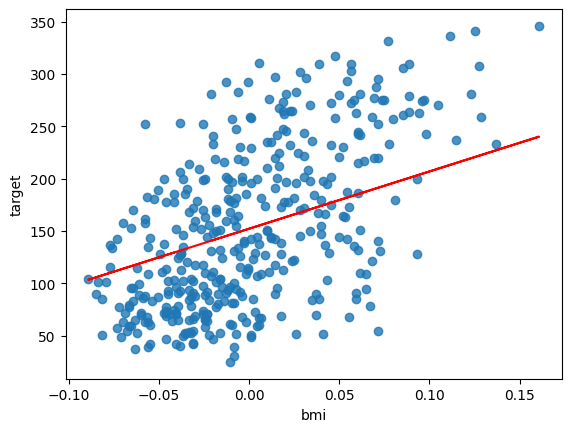
bmiとフィットした直線の関係はこの通りです。
単回帰のときとちょっと変わっていますね。
ちなみにpythonでは列の中身を0, 1, 2, …と0からカウントするので、今回bmiを2で取り出します。
精度の計算もしてみましょう。
import numpy as np
from sklearn.metrics import mean_squared_error
print(np.sqrt(mean_squared_error(y_test, model.predict(X_test))))
# ========== output ==========
# 55.0412750320784955.0と単回帰より若干悪くなっていますが、そんなに大差ないですね。
bmiが重要だったなら、それだけを使う単回帰で十分かもしれません。
まとめ
今回は線形回帰モデルの作り方を紹介しました。
初心者でも簡単に作ることができるのでぜひ自分で作ってみてください。
慣れてきたら、XGBoostやLightGBMなど、ちょっと難しめのモデルに挑戦してみましょう!



コメント